最終更新:2020/04/22
アクセス解析を見ていると、Googleなんかで結構「LightWave」で検索して飛んでくる人が結構いるみたい。たぶん、ShadeやメタセコイアやMayaなんかと比較して、どの3DCGツールが一番自分に適しているかを模索している人がいるみたい。
なので、実験的にLightWaveでのモデリングの実例を示してみようと思います。操作性の参考になれば幸いですが、基本的に『架空のメカ限定』なので、3DCGツールで実在の戦闘機や戦車を精密にモデリングしたい人、マンガ風リアル風問わず美少女をモデリングしたい人はアテにしないでください。
まず、おおまかに完成形をイメージします。人によってはデザイン・ラフを二次元の紙などに描いてから作業にかかる人もいますが、失敗が少ない代わりに時間がかかるのが欠点です。
イメージだけでモデリングを始めるのは時間が短くて済むのが長所ですが、思ったとおりにならない、つまり失敗する可能性も上がります。ですが、基本的にデザインとモデリングを同じ人がやるのであれば、
三次元のデザイン能力が二次元のデザイン能力を超えることはまずない。
ということです。
なので、ラフは描きません。経験則ですが、三次元デザイン能力が二次元デザイン能力を上回るのは、すでにプロの手によって精密なデザイン画を起こされているものを三次元化した場合に限られます。つまり、「二次創作」でしか成り立ちませんよ、ということです。
今回はドラグーンの早期警戒機装備に使うロートドームをモデリングします。E-3やE-767に装備されている実在のロートドームも直径9メートル、高さ1.8メートルくらいあるので、ひとまずそのくらいにします。
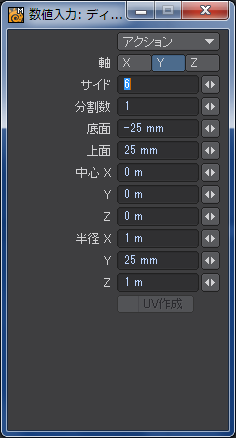
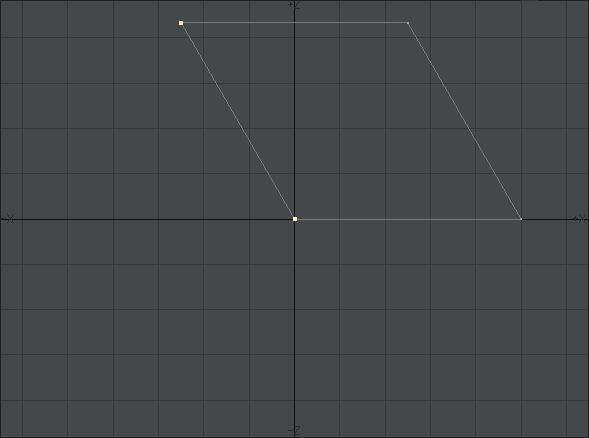
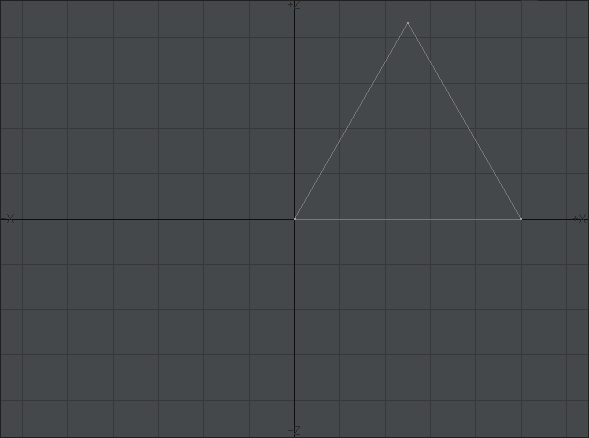
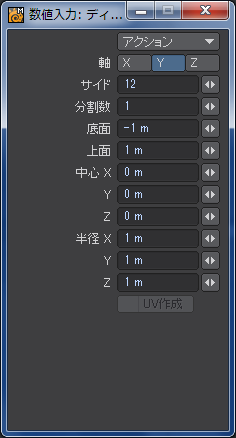
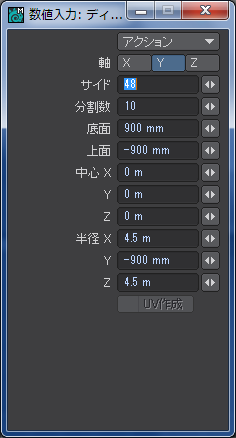
最初に「ディスク」ツールを使います。
サイドのデフォルトは24ですが、装備で一番目立つ部分なので見るからに「カクカク」なのは避けたいのと、後々のモデリングのことを考えて倍の「48」くらいにしておきます。多すぎるとモデリングが少々面倒になりますが、「ループ選択」ツールなどを使えば大した問題にはなりません。ポイントを一個ずつ選択してたらダメですよ。三次元では手を抜いても品質に影響のないところをいかに省力化するかが結構重大です。
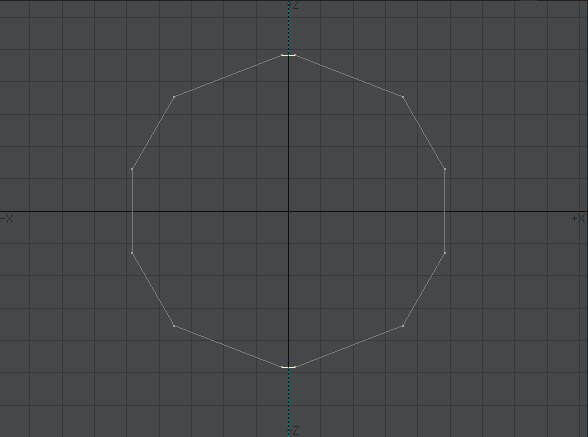
後で円盤状にするので、分割数を「10」にしておきます。上下対称にするので偶数が好ましいでしょう。
中心点の位置は別にどこでもいいのですが、後のモデリングの際に誤って中心座標を書きつぶしてしまった場合のことも考えてXYZの3軸とも0に設定しておくのが無難です。LightWaveは座標がメートル単位で浮動小数点数なので、3軸分はちょっと覚えてられません。
「ストレッチ」や「拡大縮小」や「回転」の際にもいちいち中心座標を指定しなくてよくなるのである程度形が出来上がるまでは原点でモデリングするのをオススメします。
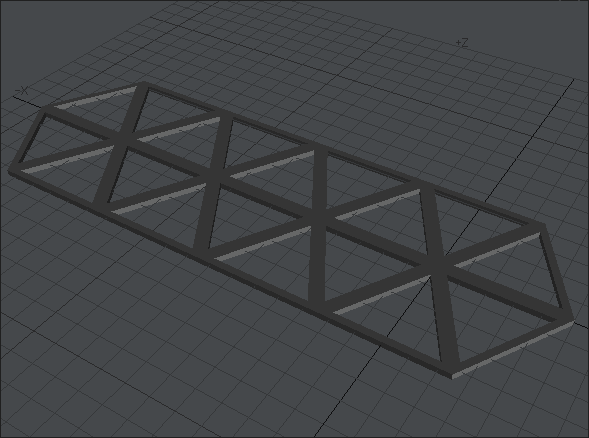
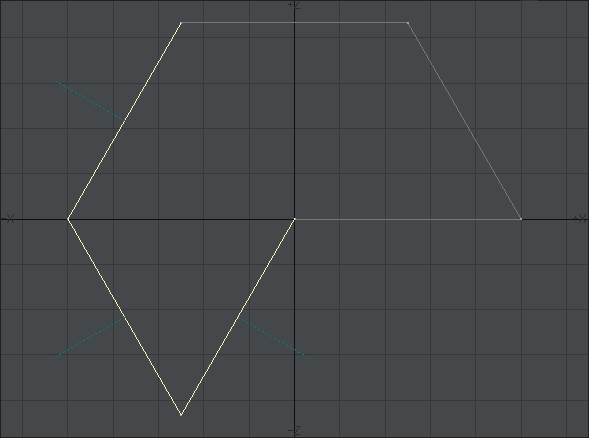
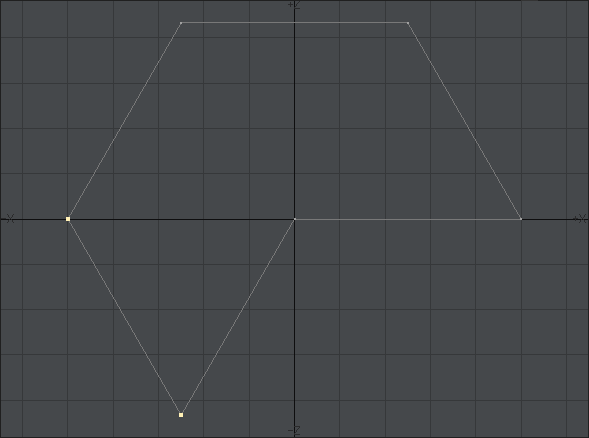
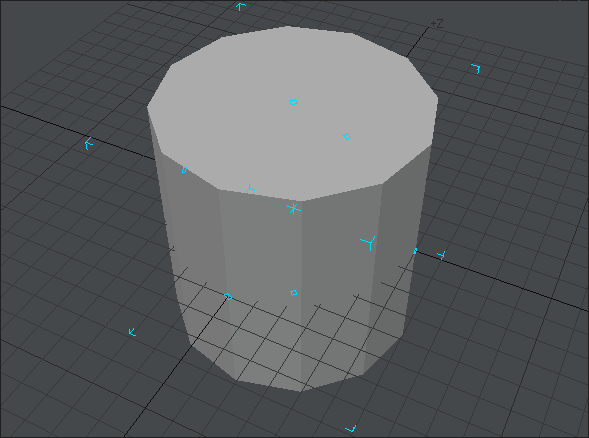
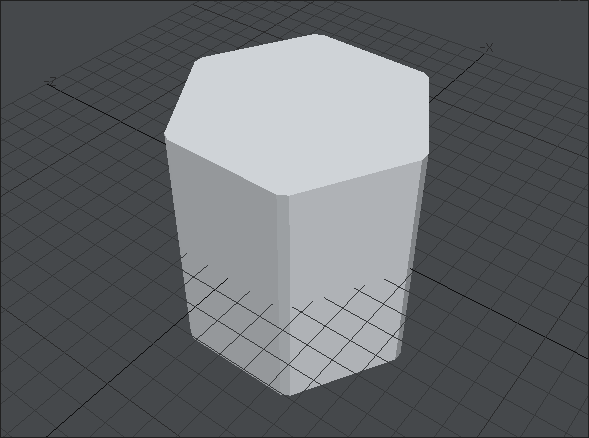
こんな形の円柱ができます。
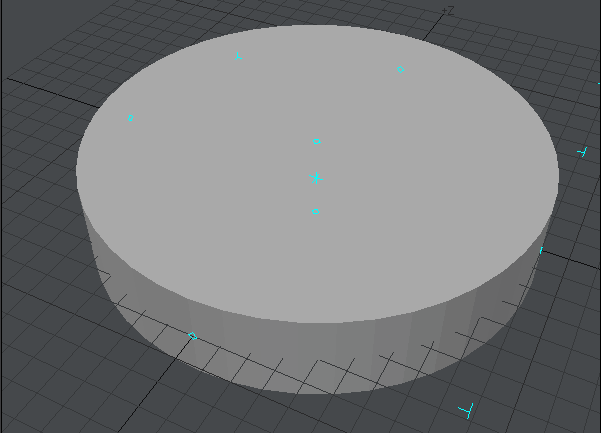
この円柱に「ベベル」や「ストレッチ」ツールを使っておおまかに形を作っていきます。細かい数値は示しません。この辺は純粋に個人の好みの問題です。
このとき、ポイント選択モードで水平に連なっているポイントを上下対称に選択して上下同時に加工していくと楽ですし、綺麗な上下対称のロードドームが作れます。

こんな形になりました。中央付近の灰色の部分が「ベベル」ツールを3回適用して作った窪みです。二次装甲の下にある一次装甲を表現するために作りました。
もっと外縁に寄っているつもりだったのですが、かなり中央寄りにできてしまったので、再度「ベベル」を繰り返して一次装甲が露出している部分を外側に繰り出します。
「ラフを描いてればこんなことにならなかったのでは?」と聞こえてきそうですが、「ベベル」機能は複数のポリゴンに適応するとポリゴン同士の境界(エッジ)にも厚さがゼロの背中合わせのポリゴンを生成してしまうので、後で消すのが面倒です。細かい部分だと無駄に神経すり減らす羽目になります。「ベベル」を使うなら、細分割されていない平らなポリゴン、この場合は最初のディスクの上底面を選ぶべきです。
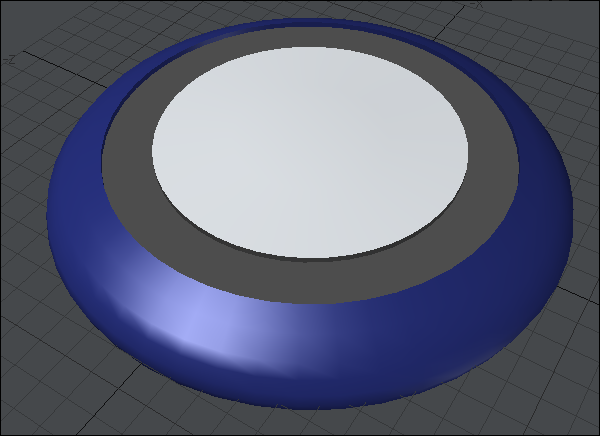
「ベベル」を二回ほど繰り返して全体の形を整えました。灰色の部分を外側に繰り出すために青色の部分を圧縮してしまったのでメッシュがかなり密になってしまいました。ディスクの分割数はもっと少なくても良かったかも。当初の予定より分厚い円盤状になってしまいましたが、まだ手直しがきくレベルですので気にしません。なんと、この状態で960ポリゴンもあります。まぁ、最近のPCは性能がいいので気にしない気にしない。可能なら「バンドグル」で統合してポリゴンを減らしてしまえばいいことです。
全体のバランスを見るためにとりあえず着色してあります。
なんとなく形はできたので、今度はSFっぽい装飾を追加していきます。

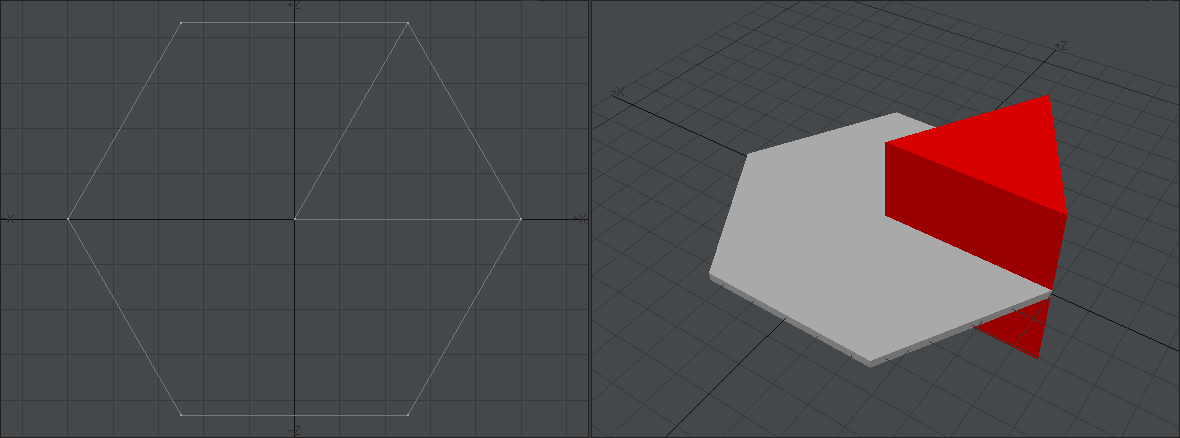
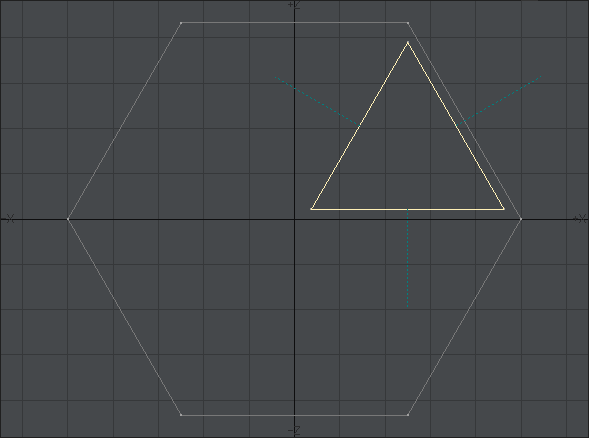
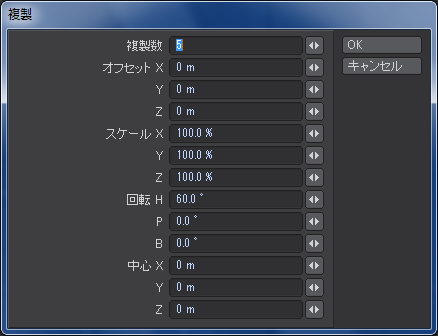
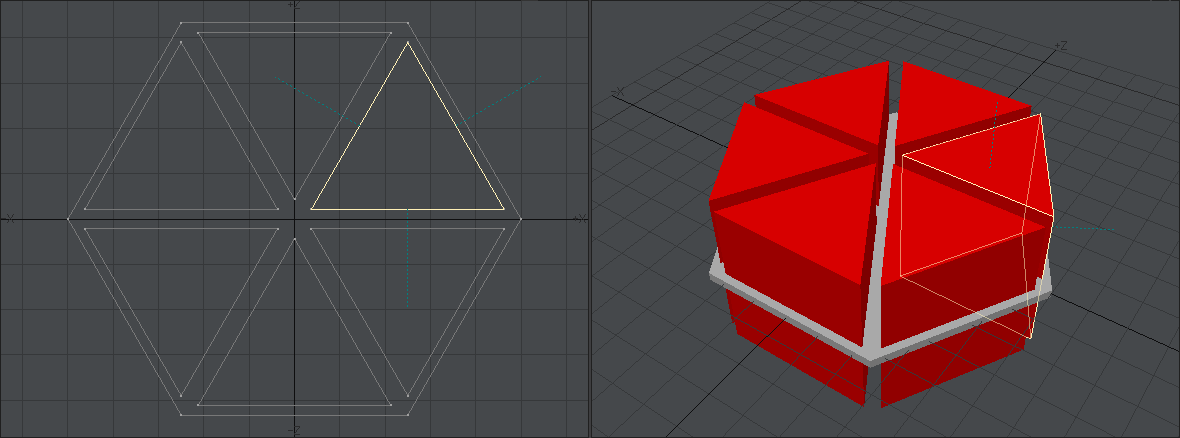
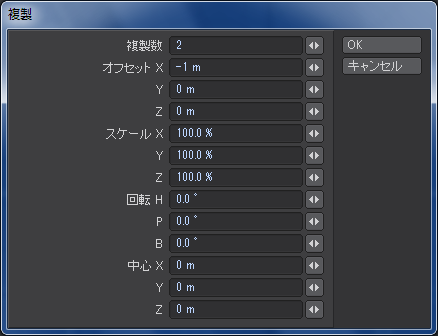
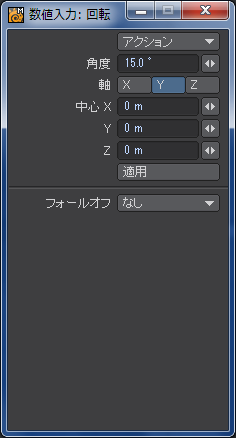
別のレイヤーに新しく正12角形のディスクを作り、それを「ストレッチ」ツールや「回転」ツールなどを使って加工したものを一旦別のレイヤーに移します。デザインがハマらなかった時のバックアップです。レドームの位置と比較しながら位置を調整した後、「複製」ツールで120度ごとに回転させて3箇所に配置しました。
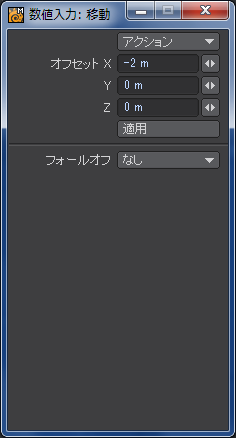
内側に押し込まれているような部分はポイント選択で該当箇所を選んで「移動」ツールで強引に内側に押し込みました。すると、ポリゴンの形に無理が出てくるので、「三角分割」で適度にポリゴンを分割して三次元的な無理を解消してあります。「三角分割」は、モデルが完成するまではOpenGLの表示がおかしくなった時だけにするなど、ほどほどにしておいたほうがいいです。
とりあえず、大雑把には完成です。せっかく広い面があるので後でテクスチャも貼ることにしましょう。
これをドラグーンに乗っけてみたらどう見えるかを見ながら調整していきます。
大体、いつもこんな感じの流れです。

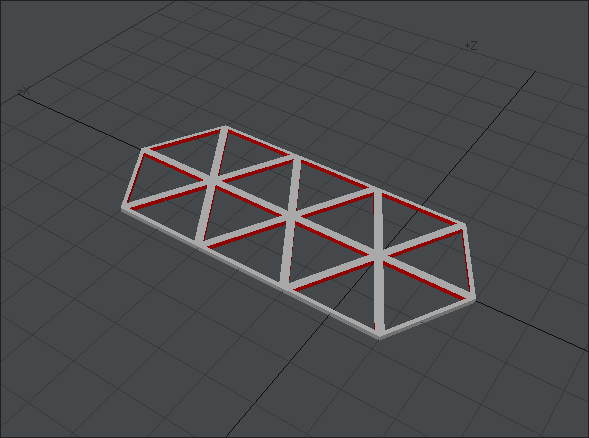
というわけで、ロートドーム完成。ポリゴンがどうなってるのか見えるようにワイヤーフレームを表示してみました。
え? 3分間クッキングじゃあるまいし、一瞬で出来たかのように完成品を取り出して「『出来上がったのがコレです』と言われても、その間の工程を知りたいんだけど…」って?
ごもっともなんですが、実在のメカを作ってるわけではないので「理想像/お手本」がなく、モデリングの手順も私個人の好みの問題が大半で、一手順ごとに細かく説明してられないんですよねぇ。ご勘弁を。
「Inkscape(インクスケープ)」というフリーライセンスのベクター画像編集ツールを使って次のようなテクスチャを作成して貼り付けてみました(Inkscapeは、ベクター画像をSVG形式で管理します。SVGはXML形式で、要するにテキストなのでファイルはかなり小さい)。Inkscapeのインターフェースはちょっとクセがありますが、Adobe Illustratorを使ったことがある人ならすぐ慣れると思います。特にテキスト・ツールは秀逸です。古いバージョンのPhotoshopやIllustratorに引けを取りません。
機能に多少の不満はあっても、なんと言っても最大の利点はタダだということです。最近、整列ツールが大幅に改善されて俄然作画がしやすくなりました。
テクスチャ・マップの画像形式はInkscapeのビットマップ・エキスポート機能を使ってPNG(Portable Network Graphics)形式で吐き出します。PNGの利点はフルカラー(24ビット)に対応していることと、アルファ・チャンネルが8ビットあるので、透過GIFと同じように透過設定ができることです。なので、地のサーフェースカラーに影響を受けないで済むのです。
LightWaveはテクスチャ・マップとして透過PNGを受け付けてくれます。レイアウトやモデラーのプレビューで使われているOpenGLも多少処理は落ちますが、表示オプションで「GLSLShaders」を選択しておけば、透過マッピングに対応できます。
JPEGでもいいんですけど、サーフェースカラーを変えたくなった時にいちいちテクスチャ画像もいじらないといけないので面倒くさいんです。とりあえず透過PNGにしておけば、レンダリングしてしまえば透過色は消えてなくなってしまいますので作業効率にはまったく影響を与えません。
PNGは不可逆圧縮のJPEGとは対照的に可逆圧縮なので画質がまったく劣化しないという特徴があります。その代わりにファイル・サイズが大きくなるという欠点がありますが、細い線や小さい点描などのテクスチャの場合はJPEGだと圧縮の際に消えたりボケてしまったりすることがあり、目的に適わないことがあります。
また、HDDの容量をキロバイト単位で節約しなくちゃいけないほどHDDに困っている人は今はほとんどいないと思います。特に三次元にせよ、二次元にせよ、PCで絵を描こうと考えてる人でHDD容量が不便な人はまずいないと思いますし。
もちろん、アルファ・チャンネルを別に用意するという手もありますけど、技術的にはかえって高度ですし、透過PNGを使う単純さには敵わないと思われます。

テクスチャの貼り方にこれが正しいという方法はありませんが、本作例の場合はY軸方向に「平面状」で貼り付けて「自動サイズ合わせ」でおおまかに位置を合わせてから画像の縦横比に合わせてX軸とZ軸を調整します。本作例では繰り返し表示する必要はないので、タイル(Tile)の指定はWidth・Heightともに「Reset」に設定しておきます。
この時に電卓(Windows標準の関数電卓でOK)を使ってテクスチャ画像1ピクセルに対してテクスチャを貼る面の単位長さを求めて縦横の長さを算出しなければならないので、初心者にとってテクスチャ・マッピングを使うことの敷居が高いと思われている原因のひとつになってます。
OpenGLでプレビュー表示を見ながら直感的に設定できるようになったので、これでも想像と数値と計算の世界で貼り付けてレンダリング一発勝負だった昔よりは遙かに簡単になったんです。
余計なお節介かもしれませんが、数学が嫌いな人に3DCGは向いてないです。特に三角関数。いや、ほんとです。紙に多角形描いてみて角度や半径からXY成分の距離を求めたりとか高校の数学Ⅰの試験問題みたいなことを普通にやらないと正確にモデリングできないんです。場合によってはかなり中途半端な角度の正弦・余弦・正接を求めないといけないこともあるし、LightWaveの座標系は浮動小数点数で、「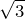 」とかでは誤魔化せないので、電卓がないとまず計算できないんです。マウス(タブレット)だけでできると思ってる人はちょっと甘いかもしれません。
」とかでは誤魔化せないので、電卓がないとまず計算できないんです。マウス(タブレット)だけでできると思ってる人はちょっと甘いかもしれません。
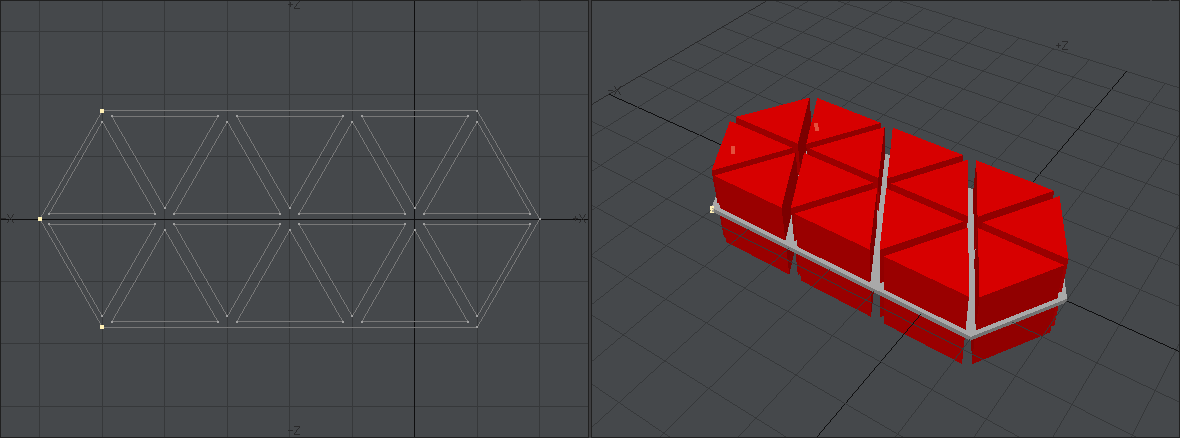
前回の記事でつけた六角形の装飾にクレーター状の穴があいてます。
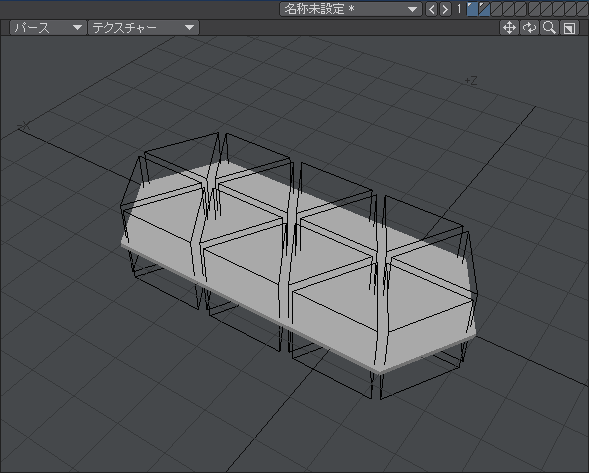
別レイヤーに保存しておいた六角形装飾のモデルの大きさに合わせて「囲い面」で穴の内周を作成して別レイヤーに置いておきます。穴の断面のさらに半分にカットしたような形にしておくのがミソです。次に「回転体」ツールを使って穴の内面を作成します。
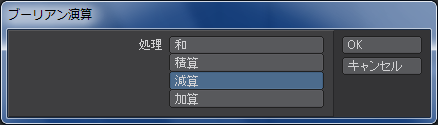
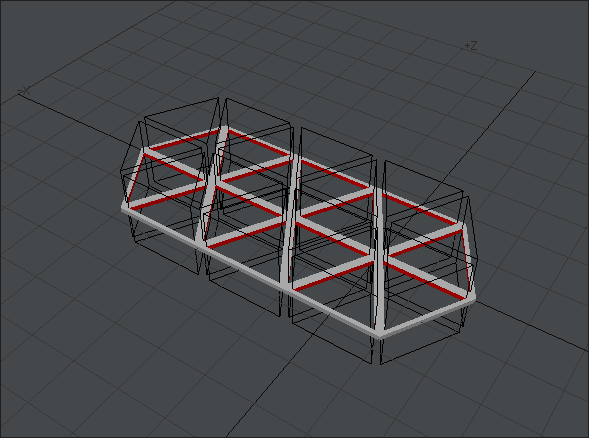
その後、六角形装飾をアクティブレイヤーに指定して、穴の内面を作成しておいたレイヤーをバックグラウンド・レイヤーに指定して「ブーリアン」ツールの「減算」モードを選択します。これで穴が作れます。
今回はたまたま何事もなかったのですが、ブーリアンをやると穴を穿った面のポリゴン構造がややこしいことになってしまいます。今回の場合、六角形装飾の表面は12角形で、穴のサイドは24なので、切れ込みが入ったみたいな、超変形36角形ということになっています。
たまに内部の数値上は穴そのものはちゃんと開いていても、OpenGLやLightWaveのレンダーが処理しきれなくて穴が綺麗に表示されないことがあります。
そういう場合は慌てず騒がず「三角分割」を試してみます。自動的に綺麗に修正してくれるはずです。よっぽど複雑な場合でない限りこれで対処できます。(12角形に24面の穴を61個開けた時も大丈夫でした。演算時間長くてフリーズしたのかと思いましたけど)
「三角分割」をした後はポリゴンの選択や編集が面倒になるので、完成間近になってこれ以上編集しないという局面になってから穴を穿ったほうがいいかもしれません。
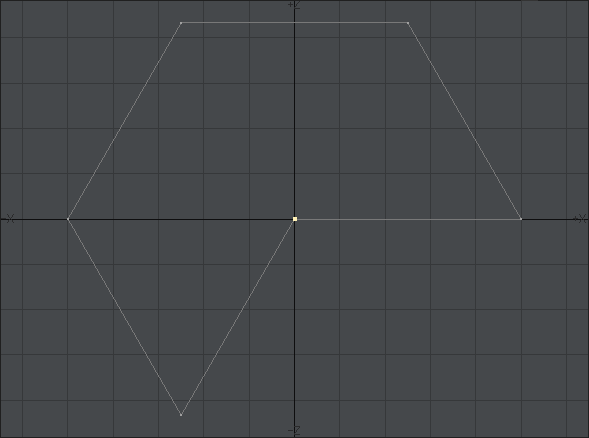
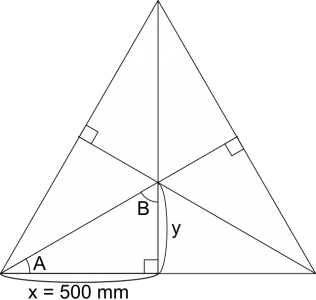
![]() は、正三角形の頂点の角度をちょうど二等分するので、30度です。
は、正三角形の頂点の角度をちょうど二等分するので、30度です。![]() は90度なので、
は90度なので、![]() は60度です。
は60度です。![]()
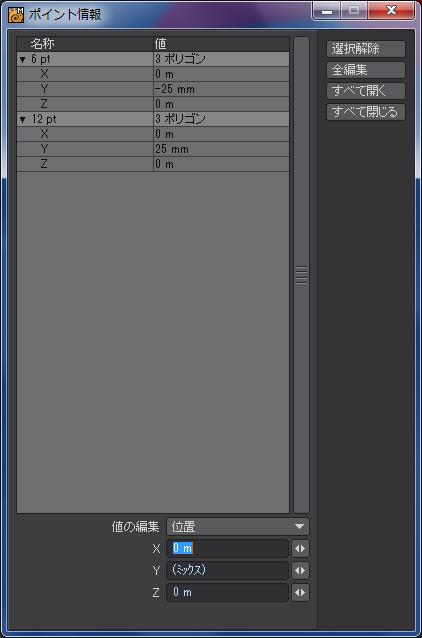
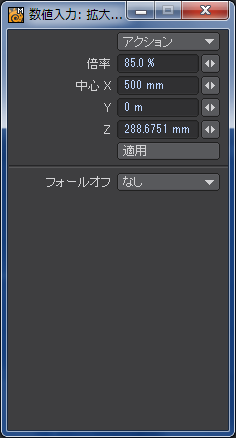
![]() 」にしてしまいましたが、入力先は「中心Z」ですのでお間違いのないよう。
」にしてしまいましたが、入力先は「中心Z」ですのでお間違いのないよう。