三角関数とブーリアン

最終更新：2020/04/22

さて、三角関数とブーリアンの話をしましょう。特にこの二者に直接の関係はないんですが、正確なモデリングをしようとすると、結構避けて通れないものなんです。

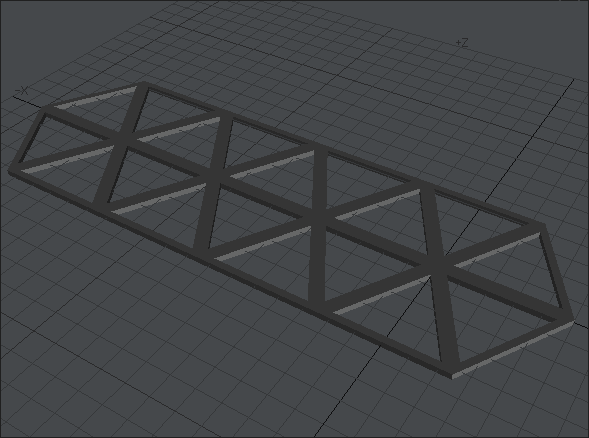
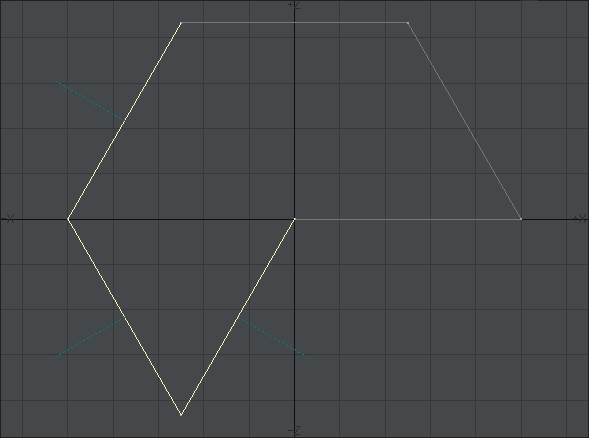
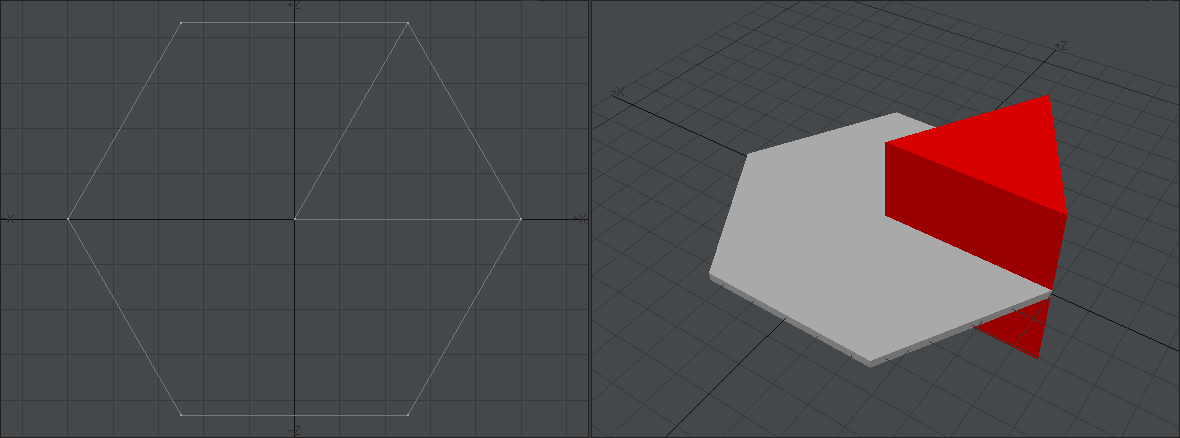
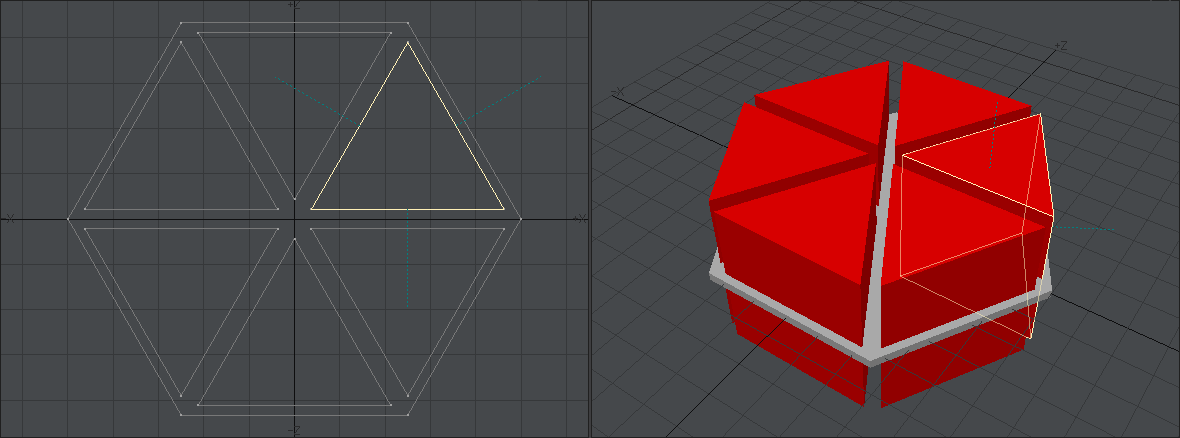
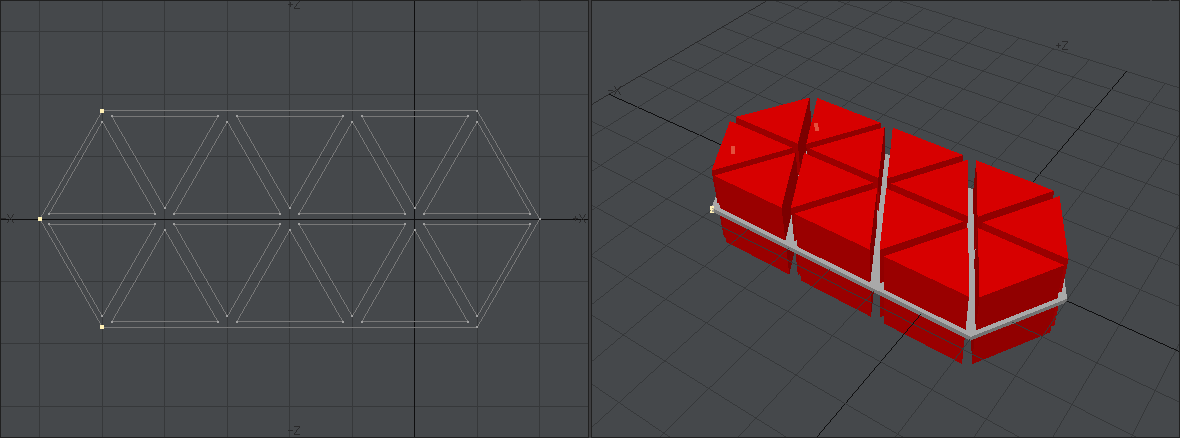
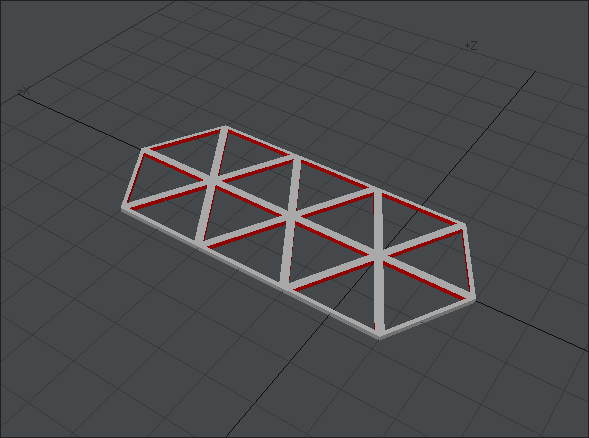
今回は完成したものを先に出しましょう。目標はこれです。これを見ただけでどうモデリングすればいいかひらめく人はこの記事を読む必要はないです。私の使っている方法が絶対正しいなんてことはないですから。

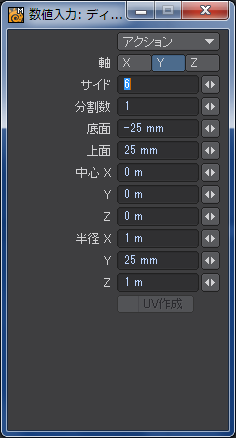
まず最初に例によって「ディスク」ツールで六角形の板を切り出してやります。厚さは50ミリメートルにしてあります。半径はこの後のモデリングに影響するので、簡単のために1メートルにしてあります。

六角形の板をコピー（Ctrl+C）でして別のレイヤーに移動して貼り付け（Ctrl+V）ます。Windowsユーザーにはおなじみの「コピー・アンド・ペースト」ですね。別レイヤーに移した六角形の板を正三角形に加工しなおします。方法はなんでもいいですんですが、多少面倒でも精度の良い方法を選択します。

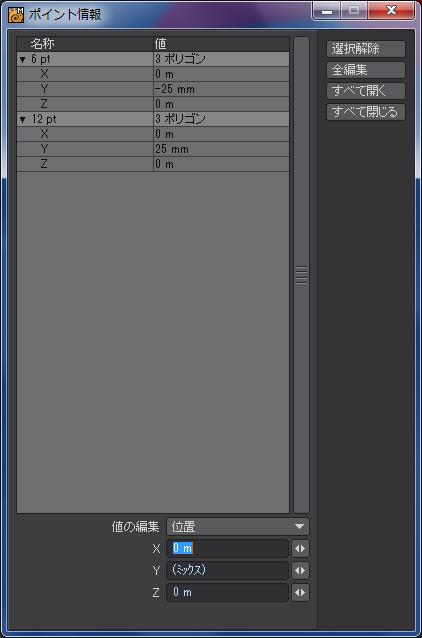
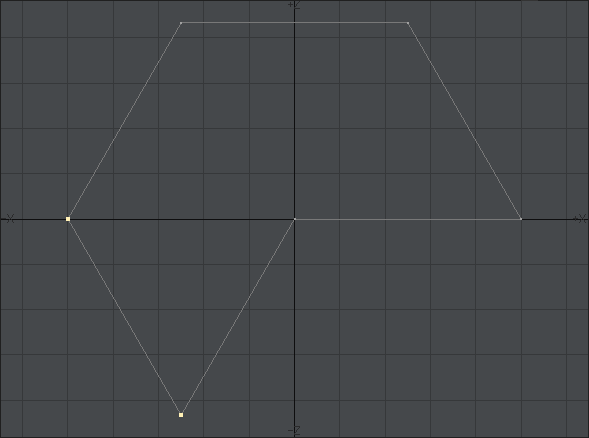
六角形の右下にある頂点をふたつとも選択して、モデラーウィンドウの下にある「情報」ボタンを押すか、キーボードの「I」を押します。上に示したような新しいダイアログが出てきたら、「全編集」ボタンを押します。X軸とZ軸の値を0に変更してダイアログを閉じます。

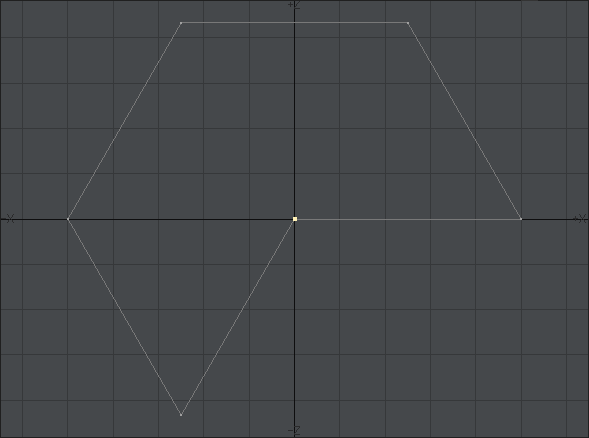
すると、次の画像のような形に変形するはずです。

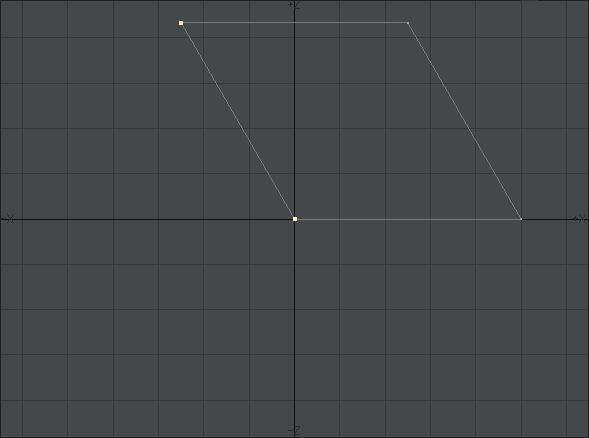
次の画像で黄色い色で選択されている3つのポリゴンは必要ないので「Delete」キーを押して消してください。

同様に、不要な頂点を消します。

次に、三角形の板に形成するために頂点の統合を行います。「詳細」タブ、「ポイント」グループの「統合」ツール（Ctrl+W）を使用します。よく使う機能なので、この際ショートカットを覚えてしまいましょう。図ではスペースの都合で上からの絵しか示していませんが、板状なので上面と底面のふたつずつ頂点があることに気をつけてください。

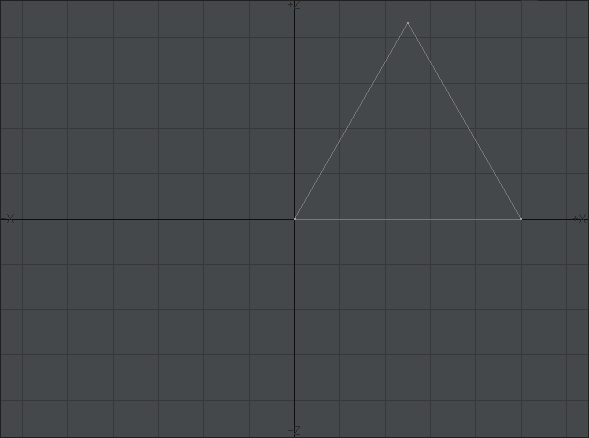
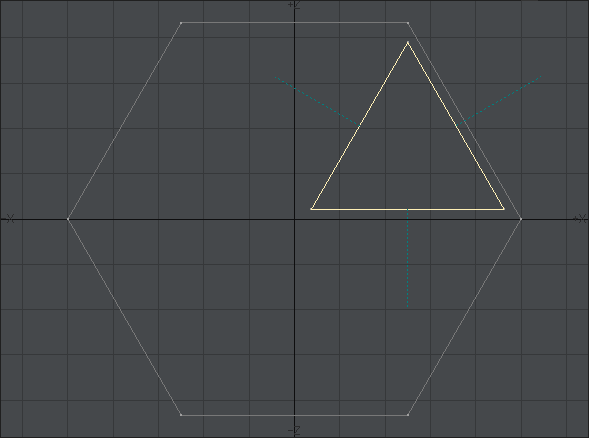
無事に加工が終わると、次の画像のような形になっているはずです。ここで重要なのは、正三角形の頂点のひとつが原点に位置しているということです。原点を頂点に持っているということは、先に作成した正六角形の中心を得たのと同じということです。

六角形の板を作ったレイヤーのボタンを「Shift」キーを押しながら選択すると、同時表示されて次のような感じで表示されます。三角形の板の上面と底面を「移動」ツールで500ミリメートルずつ上下に移動させてあります。ついでにわかりやすくするために赤く色をつけておきました。

さて、準備はここまでで、ここからが本番です。要するに、赤い三角柱で六角形の板に穴をあけたいわけですが、今のままでブーリアンをやっても、穴ではなく、三角の切り欠きのあるいびつな七角形の板ができるだけです。

そこで、穴になるべく用意した赤い三角柱を縮小します。縮小の中心位置をマウスで指定してもいいんですが、正確な位置に穴をあけることは困難でしょう。アクションの中心に「選択範囲」モードを指定しても単純に最大幅の半分になるだけで、正三角形のそれぞれの頂点からの距離が等しい中心点を得ることはできません。

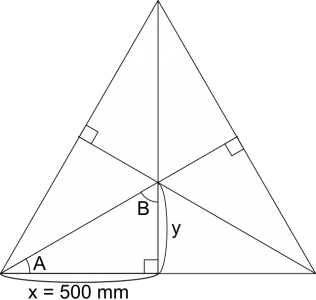
ここで登場するのが皆さんの嫌いな三角関数です。中心位置を次の図のように求めます。

六角形の半径を最初に1メートルに指定しましたから、中心位置のX成分は500ミリメートルで自明です。

正三角形の頂点から底辺に向かって垂線を引いた場合、は、正三角形の頂点の角度をちょうど二等分するので、30度です。は90度なので、は60度です。

X成分が自明なので、Y成分は次の式で求めます。

   

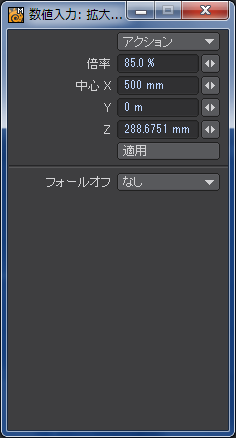
これを「拡大縮小」ツールの「中心」に入力します。

倍率はお好みで。とりあえず85%にしてあります。上の図ではついうっかり「」にしてしまいましたが、入力先は「中心Z」ですのでお間違いのないよう。

こんな感じに縮小されたらバッチリです。

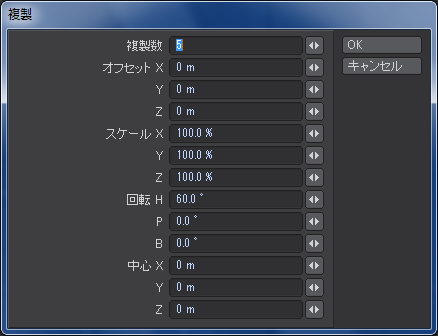
そうしたら、今度は「複製」ツールを使って、穴になる三角柱を一度に作成します。「複製数」を5に設定して、ヘディング「H」を60度に設定します。あとは変更しなくていいです。

「OK」ボタンを押して複製した結果が次の画像のようになっていれば成功です。

なんでわざわざ面倒くさい計算をしてまで中心位置を小数点以下数桁にわたって求めたか。ひとえにこの「原点を中心に回転させながら複製する」をやりたかったからなのです。一見面倒そうでも、このほうが結果的にミスが少なく、戻り作業が発生しにくく、正確かつ楽なのです。

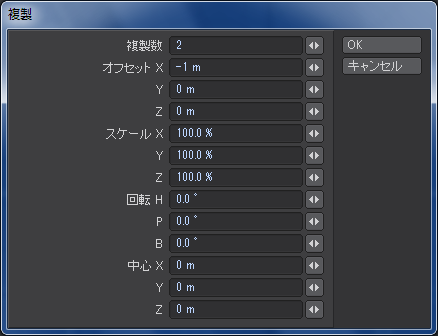
6つある赤い三角柱のうち、左の4つを選択して、さらに「複製」します。今度は「複製数」を2にして、「オフセット X」を-1メートルに設定します。ヘディング「H」は0度に戻しておいてください。

最初の正六角形の半径を入力するだけで穴が正確に複製されていくなんて、なんて素晴らしいんでしょう！

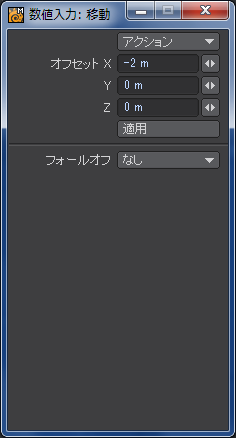
次に、六角形の板のほうの左方3つの頂点を上面、底面ともに選択して、-2メートル「移動」させます。

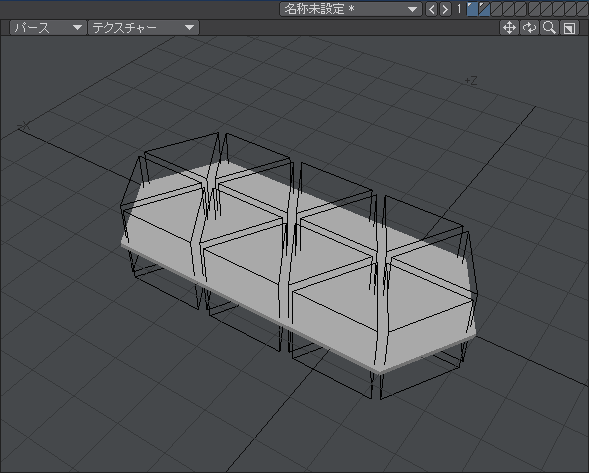
次の画像のようになっていれば完璧です。

そして、いよいよブーリアンです。六角形の板のあるレイヤーをアクティブにして、赤い三角柱群のあるレイヤーの下半分をクリックします。イメージがわかない人は次の画像の右上を見てください。こんな感じです。

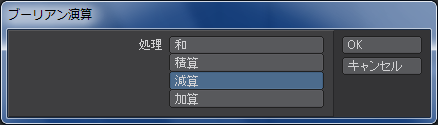
「構造」タブの「複合」グループにある「ブーリアン」を選択します。
「減算」ボタンをクリックして「OK」を押します。すると…

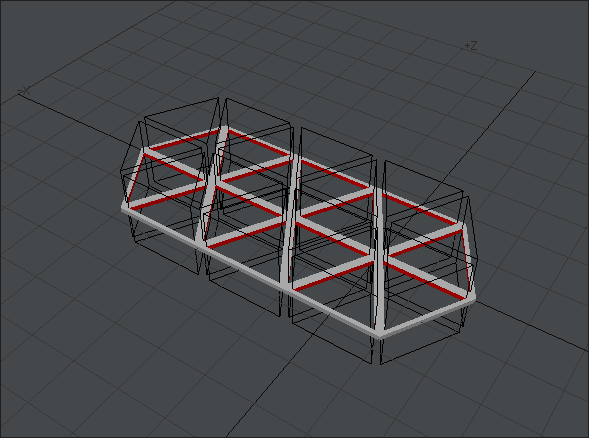
このようになります。成功です。OpenGLの表示崩れも起きていないようですね。もし、表示崩れが起きていたら「三角分割」を試してみましょう。

お気づきかと思いますが、穴を開けられた場所の面は、赤い三角柱の色になっています。これをうまく利用すれば、細かいポリゴン選択をせずとも複合的な配色が可能になります。

以上です。細かいことを言うとまだありますけど、とにかく実用上はこれで十分なはずです。
ブーリアンの真骨頂の一部と三角関数の重要さを垣間見てもらえたのなら幸いです。