最終更新:2017/01/13
今回はプリーツスカートがテーマ。なんとなくそれらしい形のものを作るのは簡単なので、学生の制服やアイドルユニットのお揃いの衣装などでお馴染みのチェック柄のスカートを作る。チェック柄なんて珍しくもないけど、チェック柄を甘く見てはいけない。
3DCG隆盛の昨今でも、チェック柄のスカートを身にまとった美少女キャラクターの3Dモデルというのは驚くほど見かけない。まず考えられる理由としては、UVマップに格子状に展開したチェック柄を歪ませないように維持したままスカートをモデリングするのが難しいからというのが挙げられる。単純に裾を広く、ウェストを細くすると上に行くほど柄が細くなってしまい、不自然になってしまう。
仮に、モデルを単純化してテクスチャの描き方を工夫するにしても、放射状に広がる裾に合わせてチェック柄を描くのは、柄の連続性をどうやって担保するのかといった問題も含め、控えめに言っても労力がかかる。立体化を前提、想定、又は期待してキャラクターデザインをする場合、チェック柄のスカートは全般的に避けられる傾向にある。現実世界では街に出ればチェック柄のスカートばかりが目立つのに、二次元世界では学園物の作品でも制服のプリーツスカートにチェック柄を採用している学校のほうが珍しい。もっとも、立体化の前にアニメ化やコミカライズといった二次元化があり、単純に描くのが面倒という現実的な問題もある。
また、プリーツスカートの縫製の特殊性にも理由がある。縫い目を切り離して展開してみると、大抵の人が想像するような扇形や台形の生地ではなく、実は長方形の布1枚でできている。それを末広がりの独特のラインに仕立てるために、「曲線折り」という特殊な折り方を採用している。ウェストが細くなるようにまっすぐに折るといずれチェック柄が斜めに傾いていってしまうのを避けられない。
本物の布や折り紙であれば基本的に伸び縮みはないので、順序よく折り目をつけていけば自然にプリーツスカートの形になっていくんだけど、3Dモデリングの場合、ポイントを移動させるとエッジがいくらでも伸縮してしまう特性があるため、エッジの長さを固定したまま折り畳むという操作がそもそも難しい。
そのプリーツスカートを現実のものとほぼ同様の発想でモデリングすることにあえて挑戦する。挑戦しないのであれば、わざわざ記事にする必要はない。例によって拡張プラスと移動ツールでモデリングしていく方法を今更紹介されても「またその組み合わせ?」と言われかねない。
基礎を作る
それでも、3DCGソフトウェアの制限には逆らえないので、まずはセオリーどおり円筒から作る。ディスク(Disc)ツールで原点に直径1m、高さ1mの標準的な大きさの筒を作る。これからややこしい計算をすることになるので、初期座標くらいは単純にしておきたい。
ひだの数があまり多いと作業が大変だし、逆に少なすぎるとプリーツスカートとは呼べなくなるので、15個とした。折り返し分を計算に入れて30面の円筒を作る。15という数字は、1周分の360°を割り切れるから。ついでに言うと、UVは幅が100%(LightWaveの内部では1.0 = 1m = 100%は等価)なので、100と360の公約数だと更に計算しやすい。とは言うものの、100と360の公約数は1、2、4、5、10、20の6つしかなく、実質10か20しか選択肢がない。
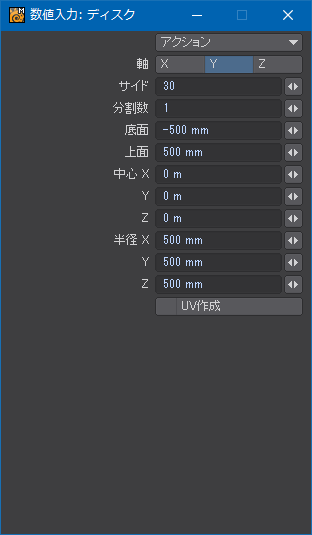
上面と底面は必要ないので、削除する。大抵要らなくなるので、「上面と底面をふさがない」というオプションがあれば便利なんだけど、些細なことなので文句を言っていても始まらない。
サーフェースがデフォルトのままだと何かと不便なので、次の画像のように「Skirt_Check」というサーフェースを割り当てておく。
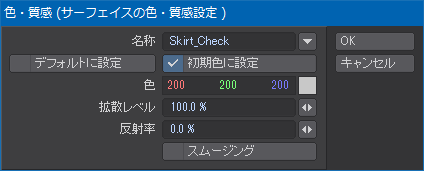
とりあえず、スムージングはかけないでおく。
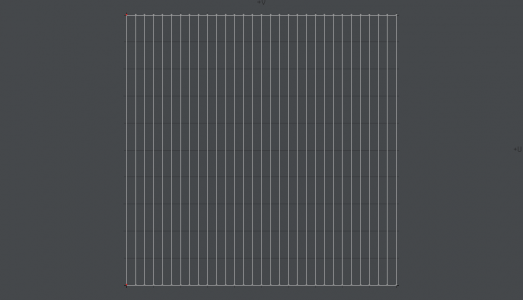
早々にUVマップを作成する。極めて単純な形状のオブジェクトなので、標準機能の新規UVテクスチャ(New UV Map)ツールで円柱状に展開する。今回の目標はUVマップを基準にしてモデリングのほうを工夫することなので、手芸店などで計り売りされている1枚布のようなマップが必要。
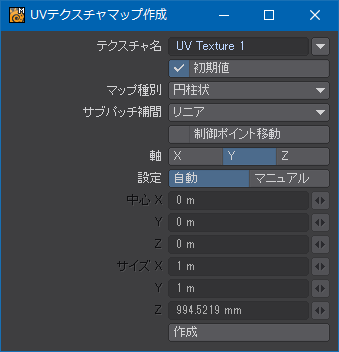
なお、プリーツの数が4で割り切れるのであれば、4分の1だけモデリングしてあとは90°ずつ回転させて複製し、境界線をつなぎ合わせればモデリングの労力をほぼ4分の1にできる。ただ、その場合のUVは4箇所とも同じ位置に重複してマッピングされることになるので、UVの扱いに慣れていて混乱しない自信があれば試してみてもいいかもしれない。それから、モデリングを済ませてしまってからUVを展開してももちろんいいんだけど、plg_Make_UV_Editなどによる自動展開は多少なりとも歪むので、UVの調整にそれなりに時間を要する。プリーツを折り畳んでしまってからLightWaveの標準機能によるUV展開は使えないと思っていい。
次の画像のような簾状のマップを作る。
更に、作成したUVにチェック柄のテクスチャを割り当てる。モデリングの説明が思いのほか長くなりそうなので、チェック柄のテクスチャの作り方はまた今度説明する。Adobe Photoshopのスマートオブジェクトはチェック柄の変更や修正に柔軟に対応できて便利なので一番おすすめではあるんだけど、レイヤーが扱えて標準的なレイヤーモードを備えている画像編集ソフトウェアであれば簡単に作れる。
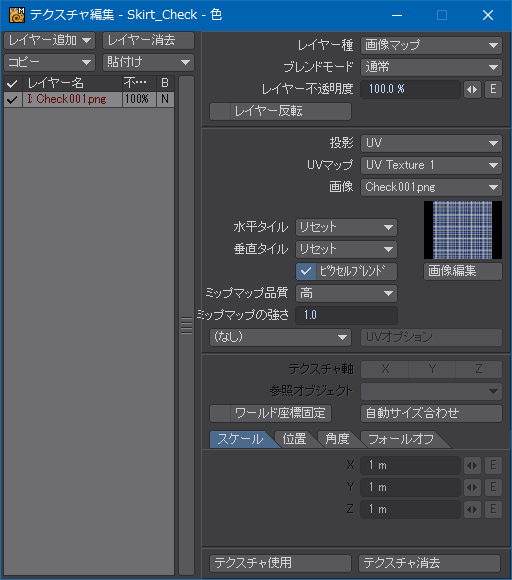
次の画像の状態が基準になる。以後、この模様が歪まないように工夫を凝らしていく。
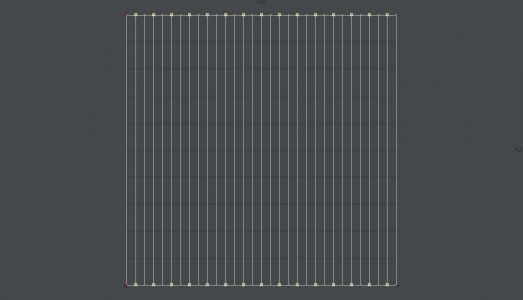
すべての面の幅が一定ではプリーツスカートにならないので、折り返す部分を短くする。次の画像のようにUVマップのビューでひとつおきにポイントを選択する。三面図の上面からのビューで選択しても同じだけど、チェック柄の連続性を維持するためにはマップの左右端にあたるポイントは間違っても動かせないので、UVマップ内で選択したほうが結果的には手早く済む。
スカートのデザインにもよるんだけど、ひだの表側に見えている部分と折り返し部分の比率は4:1にすることにした。ひだの数は15個で、現在5:5になっている比率を8:2にしたいので、![]() だけUVのU成分をずらす。UV値の変換(Transform UV)ツールで次の画像のとおりに入力する。
だけUVのU成分をずらす。UV値の変換(Transform UV)ツールで次の画像のとおりに入力する。
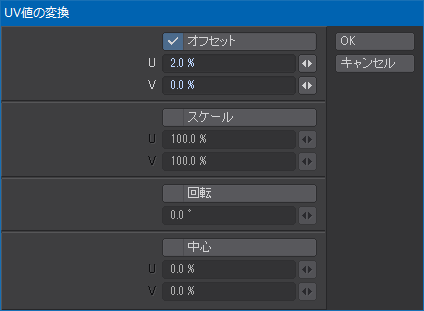
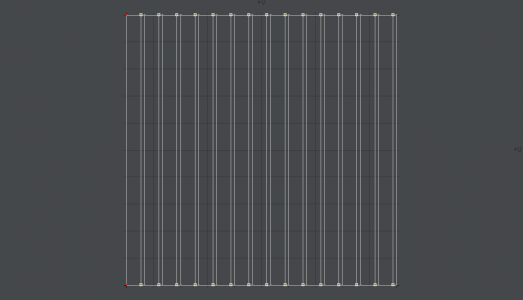
「OK」ボタンを押すと、次の画像のようにUVマップが変換される。
UVマップを変換しただけなので、三次元空間の筒の形状には変化がないけど、チェック柄が歪んでいるのが確認できる。
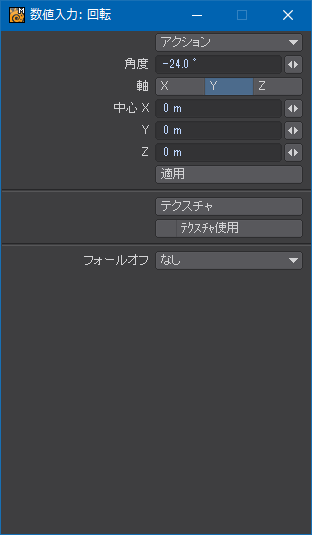
ポイントの選択を解除しないようにして、今度は三次元空間のポイントを![]() だけ回転させる。正負の方向はUVの歪みを見て判断する。
だけ回転させる。正負の方向はUVの歪みを見て判断する。
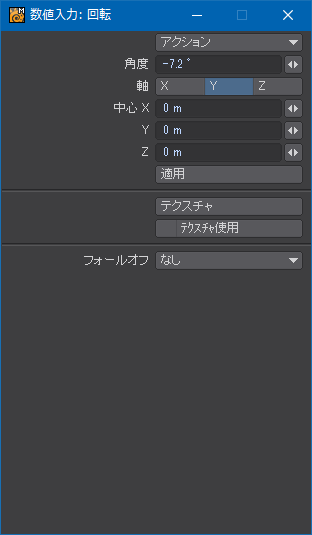
正しい方向に回転させられれば、テクスチャの見た目上は最初の状態に戻る。これでプリーツスカートを作る準備ができた。チェック柄のパターンは15×15なので縦方向が圧縮されて縦横比が一致していないけど、この段階では横方向の模様が歪んでいなければいい。
アポロニウスの円
ここからが本題。ひとつのひだを4:1に分割したまでは良かったんだけど、その比率を維持しながら折り返すのが結構難しい。比率さえ維持できていればUVを歪ませずに済むので、この際長さは変わってしまってもいい。
ここで久しぶりに数学らしい数学を利用する。
2つの点![]() と
と![]() からの距離の比が
からの距離の比が![]() で一定である点
で一定である点![]() が描く軌跡を求めたい。結論から先に言うと、その軌跡
が描く軌跡を求めたい。結論から先に言うと、その軌跡![]() は円になるんだけど、その円の中心点を
は円になるんだけど、その円の中心点を![]() とする。各点はXとYの成分を持っているので、それぞれ
とする。各点はXとYの成分を持っているので、それぞれ![]() とする。
とする。
![]() 点の座標
点の座標![]() は、次の式で求める。要は、X座標とY座標をそれぞれ別に同じ式で計算するということ。
は、次の式で求める。要は、X座標とY座標をそれぞれ別に同じ式で計算するということ。
![]()
![]() 点の座標が求まれば
点の座標が求まれば![]() 点と
点と![]() 点との距離は三平方の定理で求められるけど、今は試験問題を解いているわけではないので、ポイントの計測(Measure Points)ツールを使って簡単に求める。
点との距離は三平方の定理で求められるけど、今は試験問題を解いているわけではないので、ポイントの計測(Measure Points)ツールを使って簡単に求める。
線分![]() と
と![]() の距離が求まれば、点
の距離が求まれば、点![]() を中心とする円
を中心とする円![]() の半径
の半径![]() は次の式で求められる。
は次の式で求められる。
![]()
計算と作図がしやすいように、![]() 点が
点が![]() の位置にあるところを選んだ。これらの式から求めた数値をディスクツールの数値入力ウィンドウに入力する。座標を参照するだけなので高さは0でいい。サイドが36なのは言うまでもなく、10°刻みにするため。
の位置にあるところを選んだ。これらの式から求めた数値をディスクツールの数値入力ウィンドウに入力する。座標を参照するだけなので高さは0でいい。サイドが36なのは言うまでもなく、10°刻みにするため。
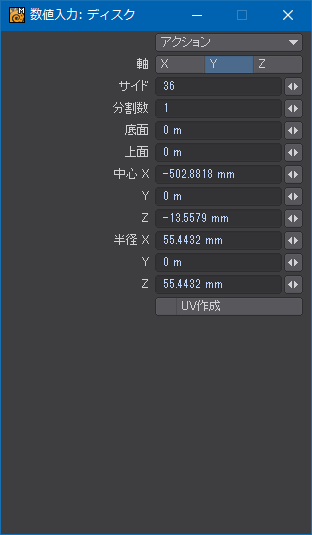
計算が合っていれば4:1の折り目で分割しているポイントを通過する円が描けるはず。実際に作図してみると思ったより半径は小さかった。精度としては4.006:1~3.995:1くらいだから誤差±0.16%前後。
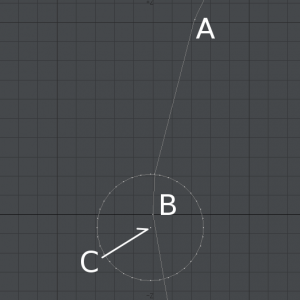
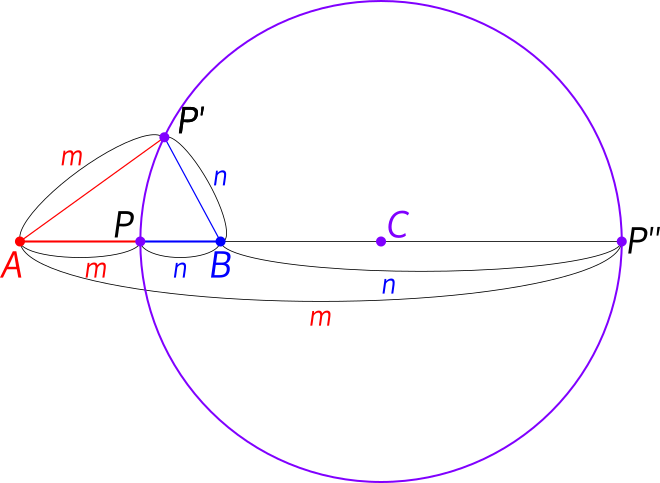
このような円をアポロニウスの円と言う。一般的には次の画像のような図で表される。図は![]() になっている。
になっている。![]() 点と
点と![]() 点が水平に一列になっていたほうが理解しやすいのでこのように描くけど、二次元的に斜めにずれていても円の位置と半径は求められる。図を見るとわかるように、比率が一定になるだけで長さまでは一定にならないことに注意。
点が水平に一列になっていたほうが理解しやすいのでこのように描くけど、二次元的に斜めにずれていても円の位置と半径は求められる。図を見るとわかるように、比率が一定になるだけで長さまでは一定にならないことに注意。
なんでこのような式になるのかまでは省略。ネットで「アポロニウスの円」を検索すれば高校の先生が詳しく証明してくれているページがたくさんある。つまり、まったく憶えてはいないけど高校の数学で習ったはずで、センター試験にも出題されるポピュラーな平面幾何学の定理。更に発展させた複素数平面を使った解法は2004年(平成16年)を最後に今の高校では教えていないらしいけど、コンピュータの発達した21世紀に生きる私がすぐには思いつかなかった方法を紀元前の数学者が既に考案していたというのだからまったく皮肉なことだ。
ある平面上で線分![]() と
と![]() の比率を一定にしたまま分割点
の比率を一定にしたまま分割点![]() を移動させたいという要求はありそうだけど、Adobe Illustratorのようなベクター画像編集ソフトウェアのツールにも意外と備えられていない。少し調べたところでは、Illustratorでもアポロニウスの円を描いてその円の外縁にスナップするようにパスの制御点を移動させるという方法が採られているようだ。
を移動させたいという要求はありそうだけど、Adobe Illustratorのようなベクター画像編集ソフトウェアのツールにも意外と備えられていない。少し調べたところでは、Illustratorでもアポロニウスの円を描いてその円の外縁にスナップするようにパスの制御点を移動させるという方法が採られているようだ。
こんな手間のかかる計算までしなくてもいいのでは、と言われそうだけど、アポロニウスの円は平面上にある2点についてしか通用しないものなので、今使わないと使う機会がなくなる。それに、いつも「適当に、感覚で」と繰り返すのでは何の参考にもならない。それほど厳密でなくても良ければ、ひだの角度を直角と仮定して三角関数の正接(![]() )が0.25になるおおよその位置を求める方法もある(あくまでも仮定なので、実際に操作すると直角にはならないため、無視できないほどの誤差が出る)。
)が0.25になるおおよその位置を求める方法もある(あくまでも仮定なので、実際に操作すると直角にはならないため、無視できないほどの誤差が出る)。
![]() 点と
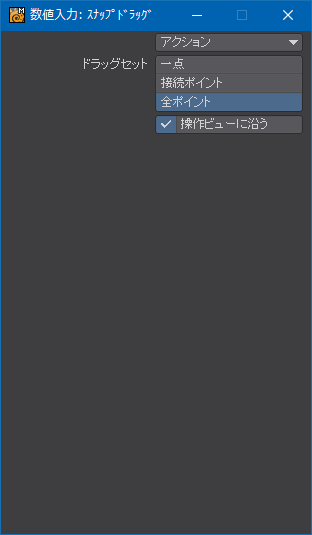
点と![]() 点の間の分割点を選択し、スナップドラッグ(Snap Drag)ツール(Shift+G)でアポロニウスの円上にある任意の点にスナップさせる。この時、「操作ビューに沿う」にチェックを入れておかないと水平に動いてくれないので注意。
点の間の分割点を選択し、スナップドラッグ(Snap Drag)ツール(Shift+G)でアポロニウスの円上にある任意の点にスナップさせる。この時、「操作ビューに沿う」にチェックを入れておかないと水平に動いてくれないので注意。
次の画像のように、4:1の比率を維持したまま折り返すことができた。
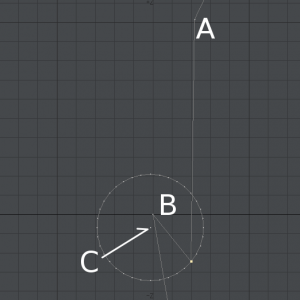
15個あるひだの数だけアポロニウスの円を作るのはさすがに大変なので、スカート全体を15分の1、つまり24°ずつ回転させて、スナップドラッグを繰り返す。原点を中心にしてアポロニウスの円をスカートの外縁を周回させても同じだけど、円周率が無理数であるために回転は誤差が蓄積しやすいツールなので、変形の基準にするものはできるだけ移動させたくない。
15個のひだを折り返し終わった状態が次の画像。ここでウェスト部分を絞ってしまうと、冒頭でも書いたようにチェック柄が先細りしてしまう。

縦横の模様を合わせる
ここでチェック柄の縦の模様を横の模様に一致させる。ひとつのひだの長さは既にわかっているので、それを15倍すると裾の周囲の長さが求められる。結果、4.4306205mと求まり、スカートの丈の長さは1mなので、裾の周囲に対する割合は![]() となる。
となる。
上端のポイントを選択し、これをUV値の設定(Set UV Value)ツールでUVのV成分に入力する。
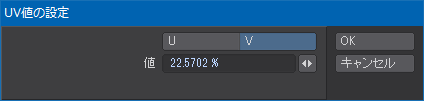
上を下に移動させたほうが計算が楽なのでそうしたけど、下を上に移動させても結果は同じ。
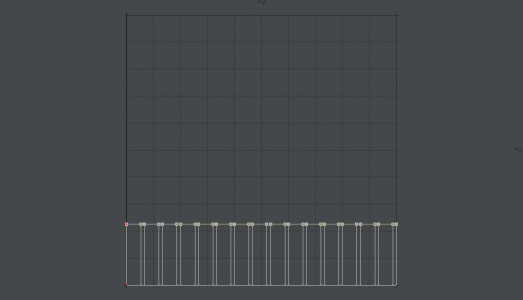
上の画像と見比べてもらえば、チェック柄の縦横比が合っているのがわかると思う。

曲線折りの模擬
次はいよいよ曲線折りを行っていく。まず、ウェストに向かって絞りたい部分を分割する。全体を半分に分割し、上半分をさらに半分に分割する。
この時、必ずバンドソープロ(Band Saw Pro)を使う。まだ単純な形状なのでナイフツールを使ってもいいような気もするし、一見すると似たような動作ではあるけど、ナイフツールはUVを壊してしまうことがある。バンドソープロが優れているところは、どんなに入り組んでいようと、ポリゴンが連続さえしていれば正確に分割できることばかりではなく、UVを破損させることがない点。

次の画像のように3分割した。

分割点をひとつのひだの10%分だけ左にずらしていく。ひとつのひだのUVにおける幅は15分の1、つまり![]() なので、その10分の1をUV値の変換ウィンドウに入力する。
なので、その10分の1をUV値の変換ウィンドウに入力する。
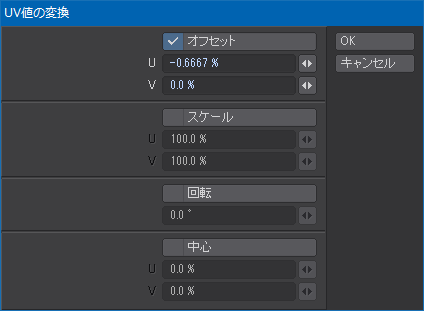
裾側から順に、![]() 、
、![]() 、
、![]() 、
、![]() になっている。
になっている。

すべての段の折り目について、アポロニウスの円を作図するのがもっとも正確な方法なんだけど、![]() 、
、![]() として単純化してみて気が付いたことがある。
として単純化してみて気が付いたことがある。
分割点が![]() 点と
点と![]() 点からの距離の比が
点からの距離の比が![]() の時、アポロニウスの円の半径は次のように求められる。
の時、アポロニウスの円の半径は次のように求められる。
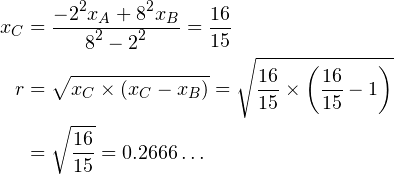
同様に、![]() の場合は次のとおり。
の場合は次のとおり。
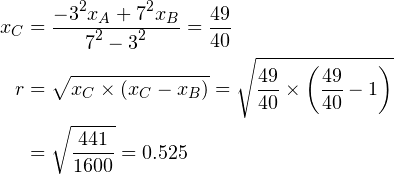
同、![]() の場合は次のとおり。
の場合は次のとおり。
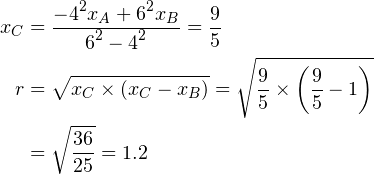
つまり、ものすごくざっくりではあるけど、比率が1割変動するたびに半径は約2倍になっている。半径の計算に平方根を使っていることに多分関係がある。円の中心点![]() は移動するので単純に2倍では本当はダメなんだけど、同じ作業を60回繰り返すのはちょっと辛いので、ある程度は近似できるということも併記しておく。
は移動するので単純に2倍では本当はダメなんだけど、同じ作業を60回繰り返すのはちょっと辛いので、ある程度は近似できるということも併記しておく。
なお、![]() の場合は
の場合は![]() なので、
なので、![]() は0になってしまい、計算できなくなる。分割点がちょうど中間の場合は、点
は0になってしまい、計算できなくなる。分割点がちょうど中間の場合は、点![]() 、点
、点![]() 及び点
及び点![]() をつなぐ三角形は二等辺三角形になり、点
をつなぐ三角形は二等辺三角形になり、点![]() の軌跡は直線になる。つまり、アポロニウスの円の半径は無限大になり、円にならないということ。とは言え、計算できないと座標が求められないので、
の軌跡は直線になる。つまり、アポロニウスの円の半径は無限大になり、円にならないということ。とは言え、計算できないと座標が求められないので、![]() の場合の更に2倍と仮定して求める。
の場合の更に2倍と仮定して求める。
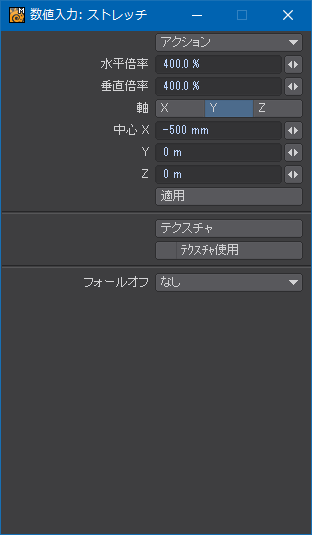
ひだの短いほうのエッジを選択し、ストレッチ(Stretch)ツール(Hキー)の中心点は![]() に固定、下から順に200%、400%、800%まで内側に向かって拡大する。
に固定、下から順に200%、400%、800%まで内側に向かって拡大する。
ウェストの絞り込み
最後に、ウェストに向かって細くなるように各段のエッジを1周分選択して縮小する。冒頭で「ウェストに向かって絞ったらプリーツスカートの意味がない」と言っていたことと矛盾するように感じるかもしれないけど、これまでの操作で上の段に行くほどプリーツの幅は広くなっているので、最後に帳尻合わせのために縮小しなければならない。エッジの長さを固定して折り畳めないならば、一度広げてから縮小して元のスケールに戻すという発想。
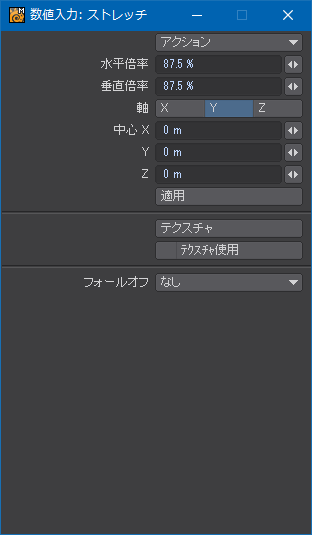
裾から数えて2段目の設定。裾のひだの長いほうのエッジが8に対して7なので87.5%と求めた。
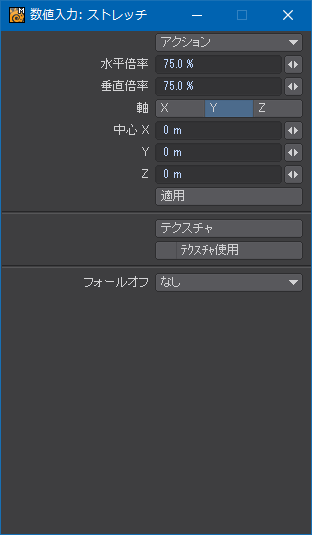
裾から数えて3段目の設定。裾のひだの長いほうのエッジが8に対して6なので75.0%と求めた。
裾から数えて4段目、つまり上端の設定。裾のひだの長いほうのエッジが8に対して5なので62.5%と求めた。
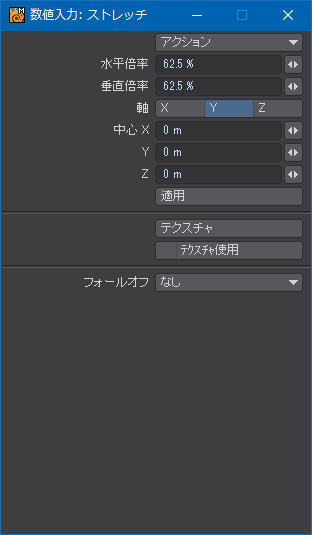
拡大してよく見てもらえればわかると思うけど、折り返し部分も含めた裾の長さの総計に対し、上の段の長さは必ずしも一定ではない。プリーツの表側と折り返し部分の比率はほぼ計算どおりなので、折り返しの角度が深すぎるために長くなってしまっている。
基本版完成
以上の操作がすべて完了してできあがったのが次の画像のようなモデル。水車のような形にはなっているけど、とてもではないけどお世辞にもスカートのようには見えない。

ところが、これにサブパッチ(キャトマル)をかけると、不思議なことにかなりそれらしいプリーツスカートに早変わりする。チェック柄もそれほど大きくは歪んでいない。見直す余地はまだあるけど、方向性は間違っていないことが確認できた。

最後に、アポロニウスの円を各段ごとに作成したという証拠物件。後でどうしても正確を期したくなった場合に再利用する。これらの円を使って作業している途中で円の半径が比率の2乗にほぼ比例することに気が付いた。

途中経過
作業のしやすさを重視して単位長(1メートル)の範囲内でモデリングしていたので、実際のモデルに着せるには大きさを全体的に拡大し、ウェストの位置とサイズに合うように調整する。あとは、多少脚がはみ出していても、物理演算でなんとかできる。
ClothFXを次の画像のように設定する。構造維持(Hold Structure)は「100」くらいにしておかないと体のラインに合うように変形してくれないのであまり上げすぎないほうがいい。一方、粘性(Viscosity)と抵抗(Resistance)をそこそこの数値にしておかないと、スカートの形状がなかなか落ち着いてくれないし、わざわざ計算までして比率を揃えたプリーツが不規則に歪むのを抑制できない。
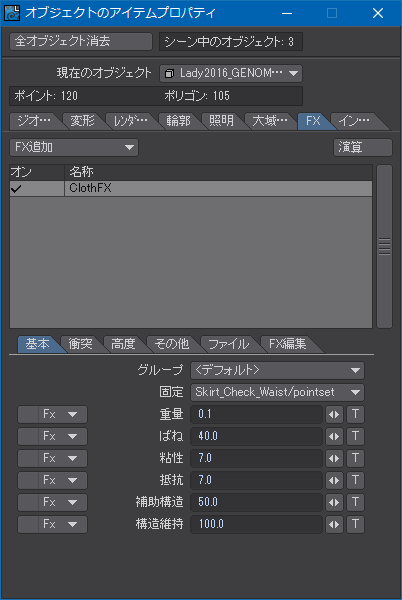
ちょっと短かったけど、いつものモデルに着せてみるとこんな感じ。
チェック柄を解除して無地にするとこんな感じ。ウェストの余裕を厳しくしすぎたために、スカート右側の一部のプリーツがモデルに貫通してしまっている。上の画像でも同様の現象は起きているんだけど、柄がなくなったので目立ってしまった。
関連記事
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―体編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―手編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―顔編1―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―顔編2―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―髪の毛編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―服装編1―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―服装編2―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―服装編3―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―ボーン編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―ボーンウェイト編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―UV編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―下半身IK編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―上半身IK編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―ClothFX編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―unReal Xtreme2編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―肌の質感編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―続・髪の毛 HairBlade編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―瞳編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―まつ毛編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―GENOMA2編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―手指FK編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―プリーツスカート編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―表情モーフ編―
- LightWaveで二次元キャラ系人物モデリング奮闘記 ―視線コントロール編―
参考記事
「プリーツスカートの展開面は長方形」という驚きの事実を再確認すべく、プリーツスカート折り紙を作る。曲線折紙はほんと面白い(まんがは「制服の幾何学」より) pic.twitter.com/lDPrQN6ApY
— こーわ (@kowa) 2016年5月4日